卧龙注册

卧龙资讯

当前位置：首页 > 卧龙资讯

常见的优化算法_1

2024-07-08 14:37:27

cost function(即代价函数或成本函数)一般为凸函数，那么什么是凸函数呢？

下面介绍数学知识：

凸函数的定义：

对区间 $[a,b]$ 上定义的函数 $f$ ，若对于区间中的任意两点 $x_1,x_2$ ，均满足：

$f(\\frac{x_1+x_2}{2}) \\leq \\frac{f(x_1)+f(x_2)}{2}$

则称函数 $f$ 为区间上的凸函数，大致图像为U型曲线，类似函数 $f(x)=x^2$ 都为凸函数。

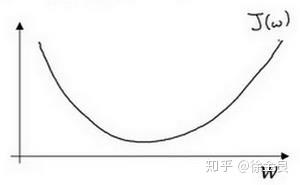
Ps:$J$函数一般指成本函数，即cost function。

判别凸函数的方法：

实数集上的函数，可通过二阶求导判断：

若二阶导数在区间上非负，为凸函数
若二阶导数在区间恒大于0，则为严格凸函数

数学介绍完毕，可略过。

梯度下降的本质就是不断循环的做下面的公式：

$w:=w-\\alpha \\frac{dJ(w,b)}{dw},b:=b-\\alpha \\frac{dJ(w,b)}{db}$

此处我们将 $w$ 看成一维的， $\\frac{dJ(w,b)}{dw}$ 就是指代梯度，也叫作斜率，也是导数。

梯度下降就是不停的使用上式更新参数，具体更新方式就是使用原有的参数值减去梯度(斜率、导数)，在减去梯度时，为了使更新粒度可控，加上一个 $\\alpha$ 超参数，这就是梯度下降过程的分析与原理。

对于一些刚接触的人来说，不明白的地方就是为何减去梯度，此处我们对减去梯度的方式进行分类验证。

假如当前点在最优点的右方，函数图像如下：

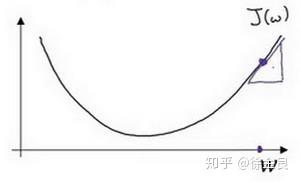
即上图三角形所在的位置，此处的梯度，我们理解为斜率可以通过高除以宽来计算，此处高为正值，宽为正值，因此斜率为正值(导数)，通过公式2计算，那么参数 $w$ 应该减小。

不断重复上述过程，当前点将会缓缓移动至凸函数的最低点，即最优点。

假如当前点在最优点的左方，函数图像如下：

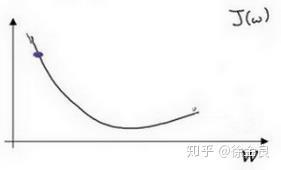
此处的斜率是负的，我们来分析一下。在此处曲线呈下降趋势，因此高为负的，宽依旧为正的，因此斜率为高除以宽，斜率为负数。根据公式进行计算，减去导数，因此参数应该变大，向右方移动，也是缓缓接近最低点，即最优点。

以上是对单个参数 $w$ 进行分析。

假如当前我们的样本属性数量为1，那么我们的模型应该包含 $w,b$ 两个参数，我们的参数更新的模型应该处于三维中，图像如下：

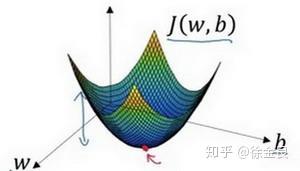
红点即为最优点，参数分别为 $w,b$ ，成本函数为 $J(w,b)$ 。

从二维到到三维，公式2同样适用，按照梯度的方向不断前进，最终会收敛到最优点或者最优点附近。

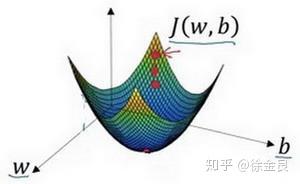
注意，以上分析中，总会有一个函数，即成本函数 $J(w,b)$ ，成本函数究竟是什么呢？

成本函数公式如下：

$J(w,b)=\\frac{1}{m}\\sum_{i=1}^{m}L(\\hat y^{(i)},y^{(i)})$

在公式3中， $m$ 代表样本数量， $L$ 代表损失函数(评估预测值和实际值之间有多接近)， $\\hat y$ 代表模型的预测值， $y$ 代表实际值， $i$ 代表样本序号。

如果在深度学习中，我们使用公式3进行模型的训练与更新，那么实际上每遍历一次样本(数量为m)，我们进行一次更新，即每epoch进行一次更新。

但是，思考一个问题，如果样本的数量很大，假如有100万个，那么更新一次样本是否太过耗时呢？

既然每次训练需要使用全部的样本太过耗时和损耗资源，那么我们可以每次使用一个样本进行更新，公式3改写为：

$J(w,b)=L(\\hat y^{(i)},y^{(i)})$

可以发现，公式4相当于公式3的简化，在随机梯度下降中，我们直接使用损失函数作为成本函数，然后再使用公式2进行 $w,b$ 的更新。

使用1个样本和使用 $m$ 个样本更新参数，除了能够减少耗时和资源意外，还有什么区别呢？

让我们通过下图进行了解：

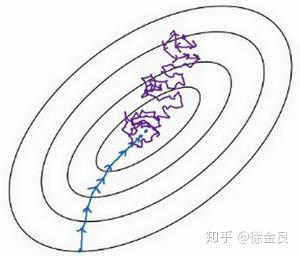
如上图所示，相当于上面三维图像的俯视图，其中中点为最优点，蓝色线是batch梯度下降的收敛曲线，紫色是随机梯度下降算法的收敛曲线。通过两条线对比可知，batch梯度下降是严格按照最优点的方向一步步稳稳的收敛的，但是随机梯度下降却显得很随意，因为单个样本点可能存在很大的噪声，有时反而向相反的方向收敛，但是整体来说还是想最优点的方向收敛点的。还有一些信息，上图没有表达出来，就是随机梯度下降虽然走了许多弯路，但是使用的总样本数和消耗的时间是小于batch梯度下降的。

因此，在样本数量极多，或者是我们想要消耗较少的资源，在尽可能短的时间收敛的话，随机梯度下降是个不错的选择。但是随机梯度下降真的没有什么缺点吗？

当然有，我们观察上图，蓝色曲线逐步到达最优点，然后稳住不动；但是蓝色曲线，也就是随机梯度下降的曲线却在最优点周围不断绕圈圈。是的！我们没看错，随机梯度下降是不会收敛到最优点然后不变动的，因为单个样本存在很大的噪声，他很难收敛到最优点。

总结：batch梯度下降一次性训练所有的样本，在样本数量大的时候消耗很大的资源，但是收敛很稳定；随机梯度下降算法每次使用单个样本进行训练，虽然下降的过程有点曲折，但是依旧朝着最优点的方向前进，使用的资源和消耗的时间相对较少。

仿佛这两种优化算法处于两个极端，有没有更好的算法呢，即不使用大量的资源去训练$m$个样本，又能消耗较少的时间，达到最优点。

当然是有的！

如名字所代表的含义，mini-batch(小批量)梯度下降，即每次使用的样本数量既不是 $m$ 个，也不是1个，它 $1<minibatch<m$ 。

我们在真实的场景中描述mini-batch算法：

加入当前我们的样本总数为500万个，如果使用500万个样本进行batch梯度下降，会消耗大量的资源和时间，但是随机梯度下降又很不准确，那么我们可以使用1000个样本训练一次，此时公式3改写成：

$J(w,b)=\\frac{1}{1000}\\sum_{i=1}^{1000}L(\\hat y^{(i)},y^{(i)})$

我们将样本分成 $5000000/1000=5000$ 份，当我们将所有的样本更新一遍后，即进行1epoch的训练后，我们的参数实际更新次数为5000次。

具体想过应该怎样呢？我们同样使用图来表示：

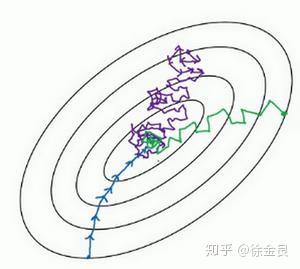
上图在batch梯度下降(蓝色)和随机梯度下降(紫色)的基础上，增加了mini-batch梯度下降的收敛曲线(绿色)。通过图片我们可以看出，它不如蓝色曲线平稳，却比紫色曲线更稳定，并且消耗的资源和时间小于紫色曲线。实际上，mini-batch的大小是一个超参数，我们可以通过控制这个超参数的大小，来实现资源和性能的平衡。

到此处，我们一共学习了三种优化算法，实际上，我们可以将他们看成一种优化算法，他们的核心就是公式2，通过梯度(斜率、导数)来进行参数的更新。

并且，batch梯度下降、随机梯度下降、mini-batch梯度下降是没有严格的优劣的，当mini-batch的大小等于m时，他就是batch梯度下降算法；当mini-batch的大小等于1时，他就是随机梯度下降算法。

对于上述三种算法的选择我们可以参考样本集的大小，如果样本集较小（小于2000），我们可以使用batch梯度下降法；如果样本集很大，我们可以考虑使用mini-batch梯度下降算法，mini-batch的数量一般为 $2^n$ ，在64到512之间。

指数加权平均，在统计学中也叫指数加权移动平均。

核心公式：

$v_t=\\beta v_{t-1}+(1-\\beta)\ heta_t$

我们来解读一下公式6，其中$v_t$表示t时刻的加权平均数，$\\beta$表示超参数， $\ heta_t$ 表示 $t$ 时刻的实际值。

我们使用具体的场景来进行解读：

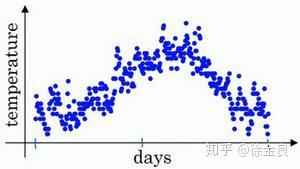
如上图所示，横轴表示天数，纵轴表示温度值，每个点就表示某天的温度值，这里有365天的数据，我们将其描画在坐标轴中。

我们按照公式2来计算每天的加权平均数， $\\beta$ 取0.9。

$v_0=0\\\\ v_1=0.9v_0+0.1\ heta_1\\\\ v_2=0.9v_1+0.1\ heta_2\\\\ v_3=0.9v_2+0.1\ heta_3\\\\ v_4=0.9v_3+0.1\ heta_4\\\\ \\cdots \\\\ v_t=0.9v_{t-1}+0.1\ heta_t\\\\$

通过每天的温度 $\ heta$ 计算每天的指数加权平均数，然后将计算后的值汇成曲线如下：

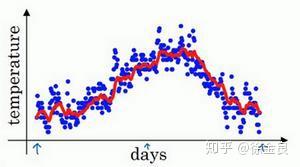
指数加权平均数在温度场景的实际意义又是什么呢？我们可以这样理解， $v_t$ 大概是 $\\frac{1}{1-\\beta}$ 天温度的平均值(前10天)，也就是红线部分所示，我们可以观察到有点右移，这就是取前10天温度的平均值作为今日温度的结果。

因为 $\\beta$ 为0.1，相当于10天的温度平均值，我们可以取大一点的 $\\beta$ ， $\\beta$ 越大， $\\frac{1}{1-\\beta}$ 越大，平均的天数越多。

按照公式7的计算方法，我们取 $\\beta$ 为0.98，绘制曲线如下：

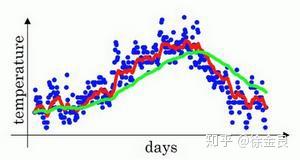
上图中的绿色曲线就是 $\\beta$ 为0.98时的加权平均数，我们可以明显看到，相比于样本数据的分布，绿色曲线向右偏移很明显，因为它平均了前50天的温度(1/(1-0.98))=50.

也许会有小伙伴好奇，如果我们把 $\\beta$ 设置的很小会怎样呢？

当 $\\beta$ 为0.5时，相当于平均了前2天的温度，经过计算，绘制曲线如下：

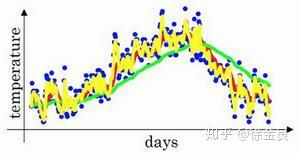
黄色的曲线即为平均前2天温度得到的，我们发现噪声非常大，但是却能够很好的适应温度的变化。

经过上述三个图的对比，说明$\\beta$是一个很重要的超参数，指数加权平均的好坏很大程度上依赖 $\\beta$ 的设置。

经过上述的场景分析，大概明白了指数加权平均到底是什么，是怎样将公式应用到实际场景中的。但是我们要知道 $\\frac{1}{1-\\beta}$ 只是一个近似值，这个近似值是怎样得到的呢，我们在此推倒一下。

$\\begin{align}v_t&=\\beta v_{t-1}+(1-\\beta)\ heta_t\\\\ &=(1-\\beta)\ heta_t+\\beta v_{t-1}\\\\ &=(1-\\beta)\ heta_t+(1-\\beta)\\beta \ heta_{t-1}+\\beta ^2v_{t-2}\\\\ &=(1-\\beta)\ heta_t+(1-\\beta)\\beta \ heta_{t-1}+(1-\\beta) \\beta ^2 \ heta_{t-2}+\\beta ^3v_{t-3}\\\\ &\\ldots\\\\ &=(1-\\beta)\ heta_t+(1-\\beta)\\beta \ heta_{t-1}+(1-\\beta) \\beta ^2 \ heta_{t-2}+\\ldots+(1-\\beta) \\beta ^n \ heta_{t-n}+\\ldots \\end{align}$

通过上式我们可以发现，无论 $\\beta$ 取值如何，加权平均数都会取之前所有的数据进行平均。那么 $\\frac{1}{1-\\beta}$ 的怎么得到的呢？

我们令 $\\epsilon=1-\\beta$ ，因此式13就可以改写成：

$v_t=(1-\\beta)\ heta_t+(1-\\beta)\\epsilon \ heta_{t-1}+(1-\\beta) \\epsilon ^2 \ heta_{t-2}+\\ldots+(1-\\beta) \\epsilon ^n \ heta_{t-n}+\\ldots?$

可以发现 $\\epsilon$ 呈指数递减， $e$ 是自然算法基础之一， $(1-\\epsilon)^{\\frac{1}{\\epsilon}}\\approx\\frac{1}{e}$ ，约等于0.34、0.35。因此，当 $n>\\frac{1}{\\epsilon}$ 时,我们可以忽略后面的值。

又因为 $\\epsilon=1-\\beta$ ，因此 $\\frac{1}{\\epsilon}=\\frac{1}{1-\\beta}$ ，我们可以用 $\\frac{1}{1-\\beta}$ 近似指数加权平均的值。

理解了指数加权平均的实际意义，其实就是求取一段时间的平均值，我们完全可以用一个移动窗口去缓存一段时间的值，然后进行求取，为何要如此费事使用指数加权平均。

原因是如果使用移动窗口，会占用大量的内存，在深度学习中，样本的数据量以及参数的数据量都是非常大的，相比而言，指数加权平均使用更小的空间和内存，是一个非常大的优势。

关于指数加权平均，还有一个知识点，就是偏差修正。

在公式7中，我们可以看到 $v_0$ 在计算时取值为0，因为按照公式，它处于初始值，之前并没有温度值。因此导致 $v_1$ 的计算结果为 $0.1\ heta_1$ ，它并没有达到我们求取平均值的目的，并且使得指数加权平均数的值很小（相比较 $\ heta$ ），从曲线中我们也可以观察到这个情况。

偏差修正就是解决这个问题的方法，它可以让初始评估更准确，具体方案是：

将 $v_t$ 换成 $\\frac{v_t}{1-\\beta^t}$ ，即：

$v_t=\\frac{\\beta v_{t-1}+(1-\\beta)\ heta_t}{1-\\beta^t}$

我们研究一下 $1-\\beta^t$ ，随着 $t$ 的增加， $\\beta^t$ 接近0，所以当t很大的时候， $1-\\beta^t$ 约等于1，偏差修正几乎没用。这正是我们想要的，我们仅想在初期通过这种方法放大平均值。

原理：

将指数加权平均数应用到梯度上，并利用取加权平均的梯度更新权重。

具体公式：

$v_{dW}=\\beta v_{dW}+(1-\\beta)dW\\\\ v_{db}=\\beta v_{db}+(1-\\beta)db\\\\ W=W-\\alpha v_{dW},b=b-\\alpha v_{db}$

此处， $v_{dW}$ 与 $dW$ 拥有相同的维数。

通过公式16我们可以发现，一共有两个超参数，分别是学习率 $\\alpha$ 和 $\\beta$ ， $\\beta$ 最常用的数值是0.9。

关于偏差修正，我们可以使用 $1-\\beta^t$ ，但是实际在深度学习中，并不会受到偏差修正的干扰，因此可以忽略。

这是momentum算法的一种形式，实际上还有另外一种，即在公式16中删除了 $1-\\beta$ ，得到的公式是： $v_{dW}=\\beta v_{dW}+dW$ ，实际上这两种形式的效果都不错，但是使用第二种方式会影响 $\\alpha$ 的最优质，对于调节超参数不是很方便，因此建议使用第一种。

以上就是momentum方法的公式和使用方法，但是为何将指数加权平均与梯度结合会有更好的效果呢？我们进行进一步分析。

下图为梯度下降的示意图：

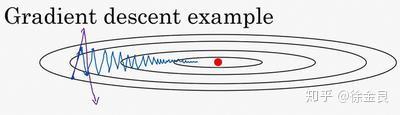
红点为收敛最优值，蓝色线为我们使用mini-batch梯度下降时的下降曲线。

观察蓝色曲线，我们可以看到mini-batch梯度下降，从横轴分析，它逐渐逼近收敛值；从纵轴分析，它因为数据的噪声产生波动。

我们想要的是它尽快向横轴的方向收敛，尽量避免纵轴的波动。

我们可以通过超参数 $\\alpha$ （学习率）进行控制吗？紫色线为实验结果，增大学习率时，它会同时影响横轴和纵轴，与我们的期望不符。

指数加权平均可以解决这个问题！！！

可以观察知识储备：指数加权平均中的图像，不正是降低纵轴上的波动，横轴上几乎不受影响。

对于梯度下降问题，使用指数加权平均后，指数加权平均在纵轴方向，会进行平均，导致正负相抵消；横轴方向都是正值，因此平均值没有太大变化。

最终的结果就是纵轴方向波动变小，横轴方向运动更快。

在横轴方向，指数加权平均实际可以理解为给了一个初始速度，，每次更新都不是独立的，因为会获取动量，这也是动量加权平均名称的由来。

类似于momentum，我们先介绍计算公式：

$s_{dW}=\\beta s_{dW}+(1-\\beta)dW^2\\\\ s_{db}=\\beta s_{db}+(1-\\beta)db^2\\\\ W=W-\\alpha \\frac{dW}{\\sqrt{s_{dW}}},b=b-\\alpha \\frac{db}{\\sqrt{s_{db}}}$

通过公式17我们可以发现，RMSprop同样使用了类似指数加权平均的原理，与momentum的不同之处体现在两个方面：

计算指数加权平均数时增加了平方操作。
更新权值时使用 $\\frac{dW}{\\sqrt{s_{dW}}}$ 的方式，而不是用 $s_{dW}$ 代替 $dW$

那么RMSprop为什么有效呢？

首先直接介绍其作用，与momentum类似，它可以减缓纵轴上的波动，同时加快，或者说不减缓横轴方向的波动。

为什么会实现上述的效果呢？同样分两步分析

计算指数加权平均数时使用平方操作，可以理解为增加了纵轴方向的波动值，横轴由于方向相同，平均数并没有显著的增加。
在更新权值时，将梯度除以 $s_{dW}$ 的平方根。在纵轴方向，由于平方的影响，纵轴方向的平均数较大，那么作为分母，使得纵轴方向的波动反而减小；横轴方向由于平均数波动不大，因此除以平方根，对于横轴方向动作影响不会太大。

momentum与RMSprop的作用类似，可以减少纵轴方向的波动，加快或者不影响横轴方向，在使用这两种优化算法的情况下，可以加大学习率，增快学习速度。

那么这两种优化算法哪个更好呢？不要急，先看下一个优化算法。

直接上公式：

$v_{dW}=\\beta_1 v_{dW}+(1-\\beta_1)dW\\\\ v_{db}=\\beta_1 v_{db}+(1-\\beta_1)db\\\\ v_{dW}^{corrected}=\\frac{v_{dW}}{1-\\beta^t_1}\\\\ v_{db}^{corrected}=\\frac{v_{db}}{1-\\beta^t_1}\\\\ s_{dW}=\\beta_2 s_{dW}+(1-\\beta_2)dW^2\\\\ s_{db}=\\beta_2 s_{db}+(1-\\beta_2)db^2\\\\ s_{dW}^{corrected}=\\frac{s_{dW}}{1-\\beta^t_2}\\\\ s_{db}^{corrected}=\\frac{s_{db}}{1-\\beta^t_2}\\\\ W:=W-\\frac{\\alpha v_{dW}^{corrected}}{\\sqrt{s_{dW}^{corrected}}+\\epsilon}\\\\ b:=b-\\frac{\\alpha v_{db}^{corrected}}{\\sqrt{s_{db}^{corrected}}+\\epsilon}\\\\$

Adam结合了Momentum和RMSprop算法，是极其常用的优化算法，本证明能够适用于不同神经网络和结构。

Adam优化算法含有较多的超参数，调优经验如下：

$\\alpha$ 学习率需要经常调试，可以在不同的实验中进行多次调试

$\\beta_1$ 超参数常用的值为0.9

$\\beta_2$ 超参数常用的值为0.999

$\\epsilon$ 常用的值为 $10^{-8}$ (为了避免分母为0而引入的值)

为什么学习率衰减能加快学习速度：

在学习初期，我们可以使用相对加大的学习率进行学习，在后期将要收敛到最优值时，如果继续使用大的学习率，那么将会在最优值附近摆动，很难精确收敛到最优值。因此，我们可以抛弃使用恒定大小的学习率的方法，使用一个衰减的学习率来控制收敛步伐。

在介绍多种衰减方式之前，介绍相关概念：

epoch：所有样本遍历一次叫做一次epoch

epoch-num:样本遍历的次数

decayrate:衰减率

学习率衰减的几种方式：

$\\alpha=\\frac{1}{1+decayrate*epoch-num}\\alpha_0$
$\\alpha=0.95^{epoch-num}\\alpha_0$
$\\alpha=\\frac{k}{\\sqrt{epoch-num}}\\alpha_0$ 或 $\\alpha=\\frac{k}{\\sqrt{t}}\\alpha_0$
离散下降(每隔一段时间减少一半)
手动衰减

常见的优化算法就是以上这些(我了解的，有新的我会继续添加)

通过上面的学习，我们已经可以将其大概进行分类了。

首先是基础梯度下降的三种：batch梯度下降、mini-batch梯度下降、随机梯度下降。

实际上batch梯度下降和随机梯度下降是mini-batch梯度下降的特殊情况，至于三种算法的选择要根据具体的需求以及数据的大小来进行抉择。

然后是梯度下降上的三种优化算法：Momentum、RMSprop、Adam

Adam是Momentum和RMSprop的结合版，也是最常用的一种，他们都以指数加权平均理论为基础，可以较少纵轴方向的波动，加快横轴方向的学习速度。

另外，为了加快训练速度，我们也可以使用学习率衰减的方式，本文也提供了集中衰减方案。

在最后，想要解释一下Momentum、RMSprop、Adam这类优化算法对于局部最优问题的益处：

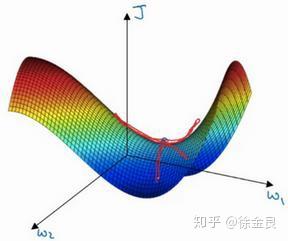
实际在我们训练过程，不太可能被困在局部最优中，相反，我们常见的问题是平稳段问题。平稳段存在于鞍点到最优值之间，简单实用梯度下降可能会在平稳段浪费大量的时间，使用基于指数加权平均的优化算法，可以加快走出平稳段，尽快训练到最优值。

金良的博客 | Jinliang Blog

上一篇：抖音极速版下载安装2022最新版下载_1

下一篇：Megatron-LM源码系列(六)：Distributed-Optimizer分布式优化器实现Part1

【返回列表】